Derivatives for Deep-Learning without math

In this post, I'll explain what the derivative is in a simplified way, and I will not mention any math equations, just pure Python code.

What Is a “Derivative”?

A derivative tells you how fast something is changing at a specific point. Imagine you have a function, like f(x) = x^2. If you pick a point, say x = 2, the derivative at that point tells you how quickly f(x) is changing right at 2.

Let me simplify it more.

Think of a function as a little machine. You put something in (input) and get something out (output). A derivative is just a way to measure how sensitive the machine’s output is to tiny changes in its input.

• If you gently tweak the input and the output drastically changes, the function is very sensitive at that point.
• If you gently tweak the input and barely see any change in the output, the function is not very sensitive there.

So, keep that in mind, a derivative ia as a measurement function because it quantifies how a function changes at any given point.

Why Does This Matter in Deep Learning?

In deep learning, we usually have a loss function that tells us how “bad” our model’s predictions are. We want to improve the model by adjusting its internal parameters (weights).

• Derivative: Tells us which direction to move those weights so that the loss goes down.
• This is like having a compass that points “downhill” so we can minimize the loss step by step.

Without this “compass,” we’d be randomly guessing how to adjust our network’s parameters. With it, we can methodically nudge them in the direction that makes our model better.

Let’s try a simple example in Python to show the concept of measuring a tiny change in input and seeing how it affects the output. We’ll define a function that just does something to an input number—without mentioning any formula. Then we’ll see how we can approximate how sensitive it is at different input values.

def mystery_machine(x):
    return x * x

This mystery_machine takes an input x and gives us an output. This is called “square function” in math.

Measuring Sensitivity

We can measure how much the output changes by doing the following:

1. Pick a spot where you want to measure sensitivity (say x_val = 2.0).
2. Record the current output.
3. Give a tiny nudge to the input. For instance, add a very small amount, like 0.00001, to x_val.
4. Record the new output.
5. Compare how much the output changed in response to that little nudge in the input.

Let's see how it works in Python:

def approximate_sensitivity(func, x, tiny_nudge=0.00001):
    original_output = func(x)
    
    # Output if we nudge the input a bit
    new_output = func(x + tiny_nudge)
    
    # How much did the output change?
    change_in_output = new_output - original_output
    
    # How "big" was the nudge?
    return change_in_output / tiny_nudge

x_val = 2.0
sens = approximate_sensitivity(mystery_machine, x_val)
print("Measured Sensitivity at x =", x_val, ":", sens)

When you run this, you’ll see a number that approximately tells you how quickly the output of mystery_machine changes around x_val = 2.0. That is conceptually what people call a “derivative.”

Let's do something else, let's create a Gradio UI that allows us to tweak the derivative function without the need to change the code:

!pip install gradio

import gradio as gr

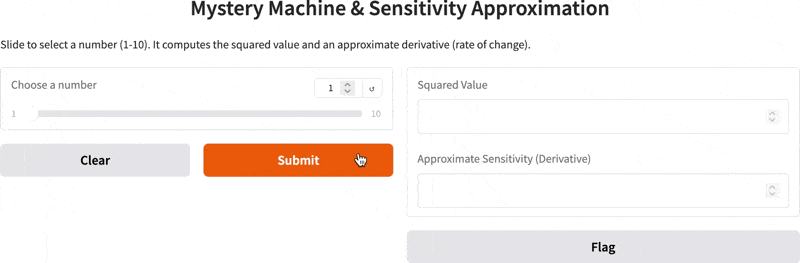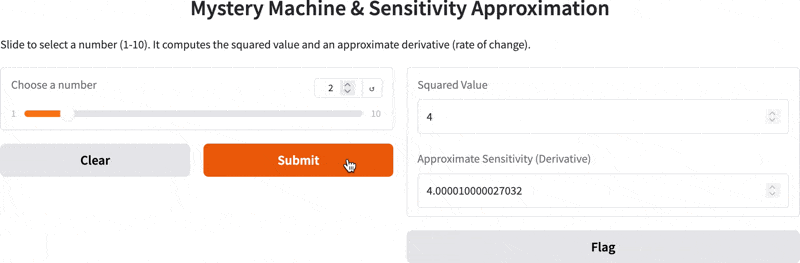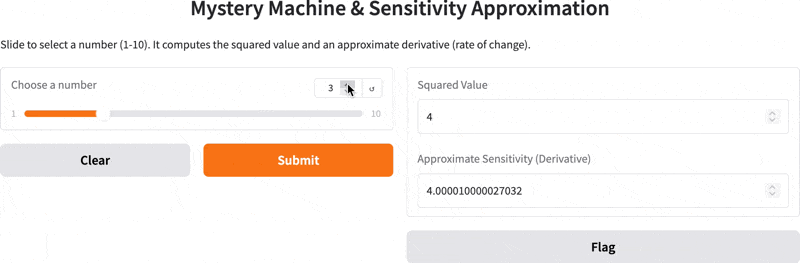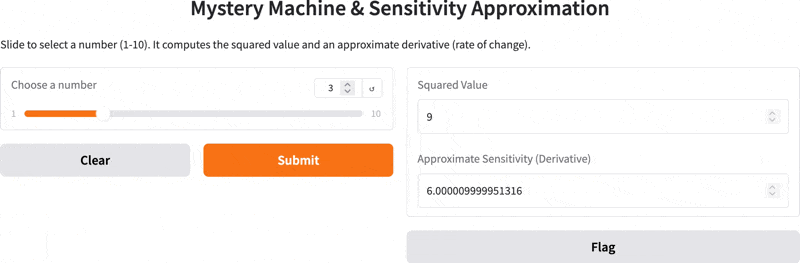
def compute_values(x):
    squared_value = mystery_machine(x)
    sensitivity = approximate_sensitivity(mystery_machine, x)
    return squared_value, sensitivity

iface = gr.Interface(
    fn=compute_values,
    inputs=gr.Slider(minimum=1, maximum=10, step=1, label="Choose a number"),
    outputs=[
        gr.Number(label="Squared Value"),
        gr.Number(label="Approximate Sensitivity (Derivative)")
    ],
    title="Mystery Machine & Sensitivity Approximation",
    description="Slide to select a number (1-10). It computes the squared value and an approximate derivative (rate of change)."
)

iface.launch()

Applying This Idea to Multiple Inputs

Deep learning models often have many parameters. Instead of a single number x, you might have dozens, thousands, or even millions of weights. The core idea still remains:

1. You take a small step in one weight (leave the others alone).
2. You see how the model’s output (or loss) changes.
3. You repeat for each weight.
4. That collection of sensitivities (one per weight) is called the gradient.

In deep learning, “gradient” usually means the value of a function’s derivative at a particular argument value.

Here’s a very basic example showing how you could measure sensitivity for each parameter in a tiny two-parameter system:

def two_param_machine(params):
    a, b = params
    return a * a + 2 * b

def approximate_sensitivity_for_all(func, params, tiny_nudge=0.00001):
    # We'll store how sensitive the function is to each parameter
    sensitivities = []
    
    # For each parameter, we do the same trick
    for i in range(len(params)):
        # Make a copy so we don't mess up the original
        params_copy = list(params)
        
        # Original output
        original_out = func(params_copy)
        
        # Nudge one parameter
        params_copy[i] += tiny_nudge
        
        # New output
        new_out = func(params_copy)
        
        # How much did the output change?
        change_in_output = new_out - original_out
        
        # Measure of sensitivity
        sensitivity = change_in_output / tiny_nudge
        
        sensitivities.append(sensitivity)
    
    return sensitivities

my_params = [2.0, 1.0]
sens_vector = approximate_sensitivity_for_all(two_param_machine, my_params)
print("Sensitivities for each parameter:", sens_vector)

This gives you a sense of how the output changes if you tweak each parameter a little bit. That’s effectively a gradient in deep learning speak, but we’re just calling it “sensitivity” here.

Tying It Back to Deep Learning

In deep learning:

• We have a loss machine (the loss function).
• We give it parameters (the network’s weights) plus some data, and it gives us a loss value.
• We measure how that loss value changes if we tweak each weight a tiny bit.
• We then adjust the weights in the direction that lowers the loss, step by step.

After many iterations of making these tiny tweaks and measuring sensitivity, the network eventually becomes pretty good at its task (like recognizing images or generating text).

Why We Usually Don’t Do This Manually

The approach shown above (“nudge and see how it changes”) can work for small toy problems, but real deep learning models might have millions of weights. Doing that for each weight individually would be extremely slow.

Instead, frameworks like PyTorch, and others use automatic differentiation, which cleverly figures out all these sensitivities in one pass—without having to do the “nudge” for each weight.

However, the concept is the same: measuring how a little change in each parameter affects the loss.

Recap

• A derivative is essentially a measure of how sensitive the output of a function is to small changes in its input.
• In deep learning, we use this notion to figure out which way to move our parameters to reduce the loss.
• The numerical example in Python shows how you might do it by trial: tweak the input just a bit, see what happens to the output, and call that your measure of sensitivity.
• For a large model, we do this for all parameters, giving us a “vector of sensitivities” often called the gradient.
• Once we have that gradient, we update each parameter in the direction that lowers the loss, slowly guiding the model toward better performance.

Final Words

Understanding “derivatives” (or “gradients”) is like understanding how to steer your car:

• Without it, you’d just drive blindly.
• With it, you know which way to turn the wheel to get where you want to go.

In deep learning, that “where we want to go” is usually minimizing the loss, and the gradient (the collection of derivatives) is the steering wheel that tells us how to get there.

That’s it—no complicated formulas or symbols needed, just the big idea:

If a tiny nudge to your input (or parameter) makes a big difference in output (or loss), your function is sensitive (high derivative). If it barely changes, it’s not sensitive (low derivative).

And that’s how we guide deep learning models toward success!